
Note: We will use abline(h = 0) to construct a horizontal line on our plot at y = 0. Once we have the residuals, we will then construct a residual plot using the plot() and abline() functions.
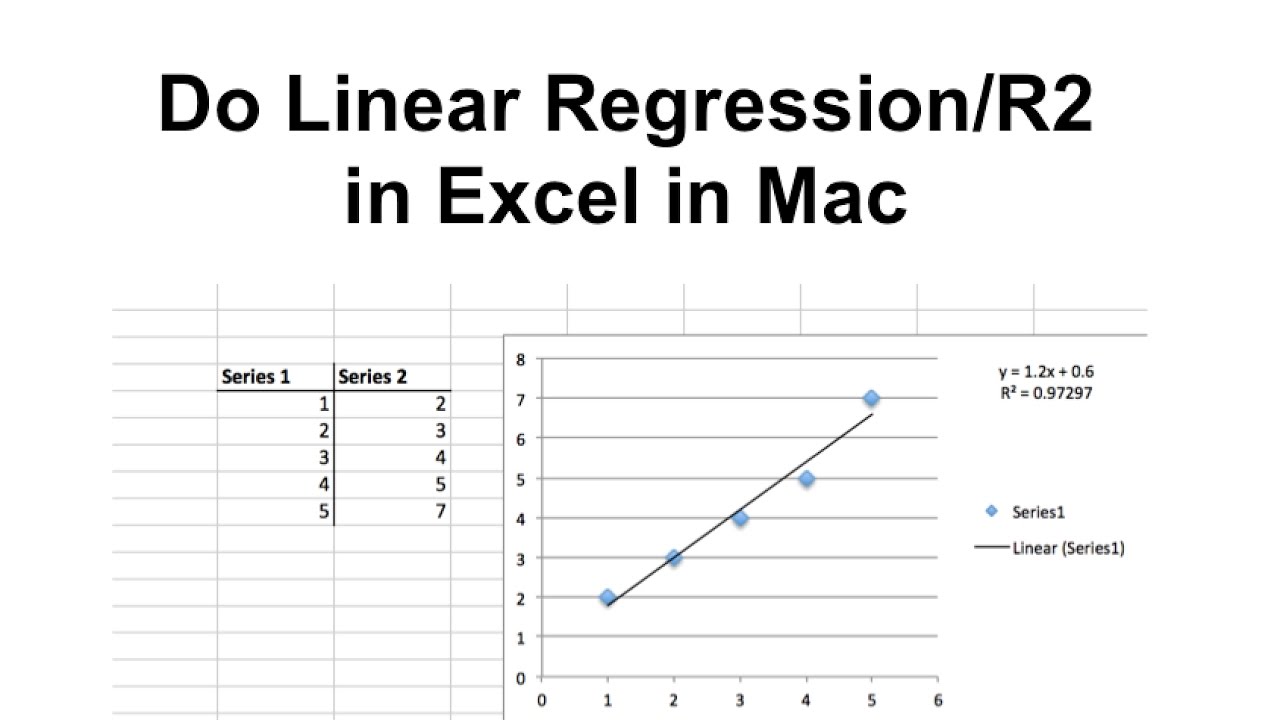
Next we will use the resid(model.name) function to calculate the residuals. Note: To perform the next step, you must have first constructed the scatterplot as shown in section I above. Now that we have constructed the scatterplot, and built and labeled the least-squares regression model, let's add the least-squares regression line to the scatterplot using the abline(model.name) function. Add Least-Squares Regression Line to Scatterplot Use the cor(x.variable, y.variable) function to calculate the correlation between the two variables. > model = lm(height ~ width)įrom the output we know that the equation for the least-squares regression: Once we create the model in R, and give it a variable name, if we call on the variable name, the y-intercept and slope will be provided. We will use the lm(y.variable.name ~ x.variable.name) function. Construct Least-Squares Regression ModelĪfter inspecting the scatterplot, it appears as though a linear regression model may be a good choice. Width (in)ī) Construct a scatterplot with fitted least-squares regression lineĬ) Calculate the correlation and equation of the least-squares regression lineīegin by entering the data into R and then construct a scatterplot: width = c(12, 15, 5, 17, 8, 10, 14, 16, 16, 9) The following data represents the trunk width and tree height of 10 randomly chosen maple trees from Leominster State Forest.


 0 kommentar(er)
0 kommentar(er)
